How to Convert Binary to Decimal?

This is a bread.

---

ANYWAY, the numeral system we always use is the Decimal System, which consists of ten different numbers:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

The Binary System is the base in computational world, to represent the bit encoded data. This numeral system only consists of 2 numbers:

0 and 1

---

Binary to Decimal Conversion

It's easier if I just put an example of this.

But before we start, to indicate the different system, usually the number has a subscript thingy so we won't be confused between those two.

Like so: 1001₂ or 11001₂ for binary numbers, and 1024₁₀ or 2357₁₀ for decimal.

Binary to Decimal Conversion Examples

• 101₂ = (1 x 2²) + (0 x 2¹) + (1 x 2⁰)

  101₂ = (4 + 0 + 1)₁₀

  101₂ = 5₁₀

• 11101₂ = (1 x 2⁴) + (1 x 2³) + (1 x 2²) + (0 x 2¹) + (1 x 2⁰)

  11101₂ = (16 + 8 +4 + 0 + 1)₁₀

  11101₂ = 29₁₀

• 1000₂ = (1 x 2³) + (0 x 2²) + (0 x 2¹) + (0 x 2⁰)

  1000₂ = (8 +0 + 0 + 0)₁₀

  1000₂ = 8₁₀

---

Did you notice the pattern? Each digit of the binary number is an increasing power of 2, starts from the rightmost to the leftmost.

The last (rightmost) binary digit is multiplied by 2⁰, then move to the left binary number, and the exponent is increased by one.

---

Binary to Decimal Conversion

This is the reversed method of the example above.

For instance:

We want to convert the decimal number 7 (7₁₀) to binary.

To do that, we iteratively divide that number with 2 and use the remainder as the binary digit.

I put a picture of the solution for that:

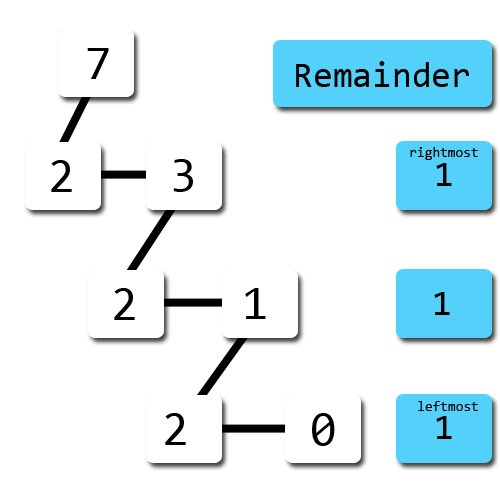
The first remainder is as the ending digit, and the last will be placed at the starting of the binary digit.

So 7₁₀ = 111₂.

---

Another example:

18₁₀ = (..?..)₂

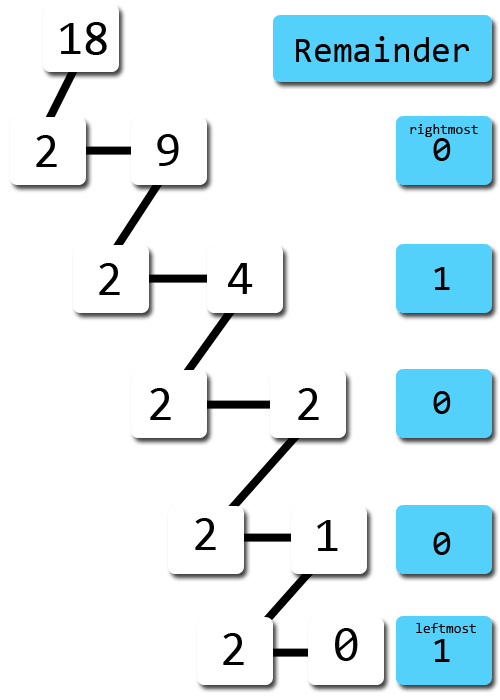
The solution of that will be 10010.

So 18₁₀ = 10010₂

---

That's about it.