Math: How to Add New Items with Equal Positional Gap Distribution to an Existing Sequence

The title is so cool. Do I get a t-shirt coupon? 😂

---

Background

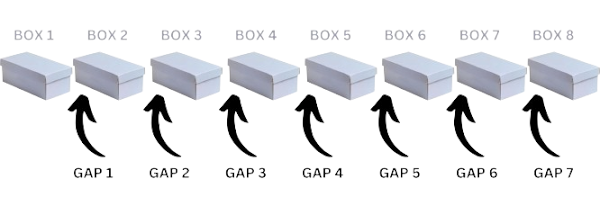
Consider we have 8 grey boxes. So, we will count the box as such 1, 2, 3, 4, 5, 6, 7 , 8

Then we wanna place another 3 new red boxes to those boxes lineup with evenly distributed gap.

How to do it?

This will be useful in programming or other engineering field that needs adding new items to that existing sequence.

I sometimes forget how to do it. Thus, I put it here as my own reminder. I hope you'll find it helpful.

It is not necessarily (directly) related to the series or sum formula for arithmetic or geometric sequence, but more to the pattern recognition and sipping some liquid while looking at the pattern 🍵🍷🍺

It's about adding new items to existing clusters, creating new clusters where the new items are distributed with roughly equal spacing between them 🐒

---

Let's Get Right to It

Again, we have box index sequence 1, 2, 3, 4, 5, 6, 7 , 8

Then, we need to add 3 new red boxes to the lineup.

The 8 boxes have 7 empty spaces or gaps (excluding the empty space before the first box and the empty space after the last box). As such:

We need to find the base positional index when the new 3 boxes are added.

$Base\_Position = (Total\_Existing\_Items - 1) / (Total\_New\_Items + 1)$

OR

$Base\_Position = {Total\_Gaps} / (Total\_New\_Items + 1)$

With $Total\_New\_Items ≤ Total\_Gaps$ and $Total\_Gaps ≥ 1$ and $Total\_New\_Items ≥ 1$

We have:

• $Total\_Gaps = 7$
• $Total\_New\_Items = 3$

Thus:

$Base\_Position = 7 /(3 + 1) = 7 / 4 = 1.75$

$Base\_Position = 1.75$

Since we get a floating number (1.75), depending on the need, we can always round that, either up or down, to nearest integer.

For this example only*, let's round up the result at this step*. Hence, we have the $Base\_Position = 2$

*More information beneath the demonstration application below 😐

When calculating the $Base\_Position$, fractional values (like 1.75 or 2.33) can't directly map to a physical gap; boxes only fit at whole number positions.

We cannot place a box at "gap 2.33" 🫠

I use the term "base" for the $Base\_Position$ because that is the first gap position in the grey boxes lineup to place the red box. This is the calculation:

• The first red box will be positioned at $2 · 1 = 2$, the 2^nd gap
• The second red box will be positioned at $2 · 2 = 4$, the 4^th gap
• The third red box will be positioned at $2 · 3 = 6$, the 6^th gap

So then, the positional calculation can be generalized as this:

$New\_Item\_Position = Base\_Position · Nth\_New\_Item$

---

Final Composition After the New Boxes Are Inserted

---

Adding New Items with Equal Positional Gap Distribution to an Existing Sequence Demonstration in HTML

Independent Demo App

Demo App Info

• Existing Boxes input is exactly that. It accepts an integer larger than 0 and less than 11.
• New Boxes input is also self explanatory. It accepts integer larger than 0 and less than 10.
• Existing Boxes must be larger than New Boxes. If not, well, it doesn't make any sense, does it? Well, it can make sense. But, you know, a bit beyond the scope of this post 😅
• Existing Gaps option is for you to look at the gap leftovers if exist.
• Hit the Calculate to calculate your inputs.
• Hit the Reset button to reset the app.

---

  Demo App Logic

• Calculate the $Base\_Position$ keep the result intact.
• For each new item position $Base\_Position · Nth\_New\_Item$ round up the result. In this JavaScript, I use Math.ceil() (ceiling method)

I put the example above (the explanation, not the app) to "simplify" it.

And I completely forgot to put this note when I published (and updated) the post.

For THAT SPECIFIC CASE ABOVE, coincidentally, either rounding up from the $Base\_Position$ or at the final result, the $New\_Item\_Position$, the result will be the same. But that's not true for other combinations. It will be completely distorted.

Apologies if you then tried the method above, then looking at the result, like, 🤔 😅

---

  Demo App Flowchart

Indeed, the loops can be merged or further simplified. This was my first take for my own explanation above. But, I suppose this separation actually helps in debugging.

---

Formalized Calculus-Style Representation

Define:

• $E = \text"Total Existing Items"$
• $N = \text"Total New Items to Insert"$
• $G = \text"Total Gaps between Existing Items"$, given by:

  $G=E−1$

• Constraints:
  $1≤N≤G$
  $G≥1, N≥1$

Base Position Calculation (Before Rounding)

The Base Position $B_p$ is determined by:

$B_p = {G} / {N+1}$

New Item Placement Formula

For each new item $k$ (where $k$ starts at 1 and increments up to $N$), the Gap Position $P_k$ is:

$P_k = ⌈k⋅B_p⌉$

where $⌈⋅⌉$ represents the ceiling function, ensuring placement in integer positions.

The Ultimate Dilly-Woo Calculus Symbolic Form For Gap Position $P_k$

$P_k =⌈k⋅ {G}/{N + 1}⌉, for\ k∈[1,N]$

Where:

$G=E−1,1≤N≤G,G≥1,N≥1$

😶

---

How Did You Come Up With That Gap Formulation?

I didn't.

Well, that's a short paragraph.

---

For uneven insertion, they will look awkward of course. But I hope you get the general idea of it.

Unevenness can happen at certain threshold of gaps and new boxes combinations. For instance, 7 boxes being inserted another 3 boxes, 5 boxes being inserted 1 new box, 4 boxes being inserted another 2 new boxes, and so on.

---

Where Is This Concept Used?

In this article (and the demonstration) for sure.

And for more implementation generic examples:

• Frontend Layout

  Dynamically positioning elements (e.g., banners, widgets, or ads) within a layout to maintain balanced spacing.

• Load Balancing in Distributed Systems

  Evenly distributing tasks or requests across multiple servers or nodes to prevent overloading.

• Electrical Engineering (Circuit Component Placement)

  Arranging components like resistors, capacitors, or inductors with equal spacing on a PCB for optimal layout and minimal interference.

• Civil Engineering (Bridge Suspension Cable Distribution)

  Determining equal intervals for suspender cables on bridges to achieve uniform load transfer to main cables.

• Grocery Store and Supermarket

  Right? You don't see the goods lying around aimlessly on the shelf and floor. They need to be neatly placed with equal positional gap distribution 😎

---

Attributions

• Grey box link
• Red box link
• I was listening to A'Studio — Тик-так on loop when creating this post.

---

Thank you for visiting. See you again.