Methods
To find the roots (the solution), we can choose between these four different methods :
- Factoring
- Completing the square
- Using quadratic formulation
- Drawing the graph : this can be achieved by writing your own loop-n-plot computer script, or using pre-programmed Mathematical software, or just using a pencil and a paper then create a table of values, continued with plotting the values on the Cartesian plane (2D x-y axis).
A glimpse about the function f(x) graph
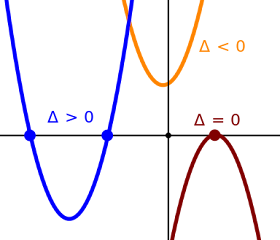
Discriminant (∇)
This is the expression that will tell us if a quadratic function crosses an axis. Because this is f(x) (the function of x values axis), then the discriminant here will tell us whether a function crosses the x-axis, touching the x-axis on one point, or floating above/below the x-axis.
For the quadratic equation ax² + bx + c = 0, the discriminant is defined as :
∇= b² - 4ac
The constant numbers a and b are the numbers (value) that represent the sum of the variables x² and x, respectively. And the c is the constant number of a quadratic equation.
Also, with this discriminant expression, we can find out if a quadratic function graph (or the equation) has two real numbers roots, two complex numbers (or just imaginary) roots, or twin real numbers roots.
For example :
2x² + 7x + 5 = 0 has a = 2, b = 7 and c = 5.
So the discriminant of that thingy is
∇ = b² - 4ac
∇ = (7)² - 4 * 2 * 5
∇ = 49 - 40
∇ = 9 ( ∇ > 0 : this quadratic equation crosses the x-axis, it has two real numbers roots)
The discriminant values :
- ∇ > 0 : the equation has two real numbers roots, the function graph crosses the x-axis
- ∇ < 0 : the equation has two complex numbers roots, the function graph doesn't touch the x-axis.
- ∇ = 0 : the equation has twins real numbers roots, it touches the x-axis on exactly one point.
The a constant
a > 0
As you can see on the graph above, it plots the y = x² - x - 2 function. The a constant of that function, the sum of x², is 1. Therefore, a = 1 or a > 0. It means the graph shape will have a valley, also means, it has a minimum value. On this quadratic non-linear equation (function), we can't have the a as 0. Why? Because, that's why.
OK, let's take a look : ax² + bx + c = 0, if we substitute the a with 0, then it will become bx + c = 0.
The last equation loses its manhood, that is its quadratic thingy, it becomes a linear equation.
So there, because.
The values of a
- a > 0 : the graph has a valley (pointing downward - opening up) with a minimum value
- a < 0 : the graph has a peak (pointing upward - opening down) with a maximum value
Methods to find the roots
The general formulation to get the roots (the solution) of a quadratic thingy is using :
For example, find the roots of this equation :
2x² + 7x + 5 = 0 ► with a = 2, b = 7 and c = 5.
Let's solve that using quadratic formulation :
x = [ -7 ± √( [7]² - [4 * 2 * 5] ) ] / 2 * 2
x = [ -7 ± √(49 - 40) ] / 4
The general formulation to get the roots (the solution) of a quadratic thingy is using :
For example, find the roots of this equation :
2x² + 7x + 5 = 0 ► with a = 2, b = 7 and c = 5.
Let's solve that using quadratic formulation :
x = [ -7 ± √( [7]² - [4 * 2 * 5] ) ] / 2 * 2
x = [ -7 ± √(49 - 40) ] / 4
x = [ -7 ± √9 ] / 4
x = [ -7 ± 3 ] / 4
x1 = [ -7 + 3 ] / 4 ∨ x2 = [ -7 - 3 ] / 4
x1 = [ -4 ] /4 ∨ x2 = [ -10 ] / 4
x1 = -1 ∨ x2 = -(5/2)
∴ The roots of 2x² + 7x + 5 = 0 are x1 = -1 or x2 = -(5/2), simplified as x = {-(5/2) , -1}
I'll show you another one, the factoring method.
Factoring
Let's take an example from the previous one : 2x² + 7x + 5 = 0 with a = 2, b = 7 and c = 5.
Continue
So we have 2 and 5 there, we put this general formulation to solve that :
Keep in mind that the equation is 2x² + 7x + 5 = 0 has a = 2.
And also, we have already got value1 = 2, and value2 = 5.
Then we can simplify that as :
(x + 1)(2x + 5)
We put it back to the complete equation, so :
2x² + 7x + 5 = 0
(x + 1)(2x + 5) = 0
x1 = 0 - 1 or x2 = (0 - 5)/2
x1 = -1 or x2 = -(5/2)
The solution, x = {-(5/2) , -1}*
*the same result compared with using quadratic formulation earlier
Anotha example :
Let's find the roots of this quadratic equation
-5x² + 24x + 5 = 0
1st step
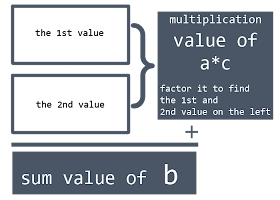
Find two numbers which if multiplied will have the same value of a*c, that is (-5)*5 = -25, and if added will give the same value of b, that is 24.
From the image above we find that the value1 = (-1) and value2 = 25.
2nd step
Put those values into the basic factorization formula :
So :
Simplify that into :
(-5x - 1)(x - 5)
Last step
Put that back in to the original complete equation :
-5x² + 24x + 5 = 0The solution, x = {-(1/5) , 5}
(-5x - 1)(x - 5) = 0
x1 = (0 + 1)/(-5) or x2 = 0 + 5
x1 = -(1/5) or x2 = 5
Other forms "shortcuts" :
- ax² + bx = 0 ► x (ax + b) = 0 ► x1 = 0 ∨ x2 = -(b/a)
- ax² - bx = 0 ► x (ax - b) = 0 ► x1 = 0 ∨ x2 = b/a
- -ax² - bx = 0 ► (-x)(ax + b) = 0 ► x1 = 0 ∨ x2 = -(b/a)
- -ax² + bx = 0 ► x (-ax + b) = 0 ► x1 = 0 ∨ x2 = b/a
- ax² - c = 0 ► ( √a·x + √c )( √a·x - √c ) = 0 ► x = ±( √c / √a )
- -ax² + c = 0 ► ( √a·x + √c )( -√a·x + √c ) = 0 ► x = ±( √c / √a )
- etc
Try out these :
First Problem : x² - 81 = 0
☺Second Problem : x² + 8x + 7 = 0
☺Third Problem : 3x² + 5x + 2 = 0
hint: type fraction like -1/2 or 2/7 etc
☺Fourth Problem : -2x² + 8x = 0
☺Last Problem : x² + 169 = 0
hint: use i for imaginary number, for instance 2 - 3i or 7i
☻Have fun... I hope.

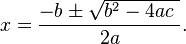

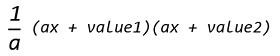




No comments:
Post a Comment
Tell me what you think...